-: matfaust::factparams::ParamsHierarchicalRectMat Class Reference

The simplified parameterization class for factorizing a rectangular matrix with the hierarchical factorization algorithm. More...

Public Member Functions
function	ParamsHierarchicalRectMat (m, n, j, k, s, varargin)

Public Member Functions inherited from matfaust::factparams::ParamsHierarchical
function	ParamsHierarchical (fact_constraints, res_constraints, stop_crit1, stop_crit2, varargin)
	Constructor. More...

Public Member Functions inherited from matfaust::factparams::ParamsFact
function	ParamsFact (num_facts, constraints, varargin)

Static Public Member Functions
static function	createParams (M, p)

Static Public Member Functions inherited from matfaust::factparams::ParamsFact
static function	factor_format_str2int (factor_format)

static function	parse_opt_args (cell_args, opt_arg_names, opt_arg_map)

static function	get_constraints (constraints)
	Returns a cell array of constraints from constraints which is a ConstraintList or cell array that can be a mix of pyfaust.factparams.ConstraintGeneric or pyfaust.proj.proj_gen. If projs is a ConstraintList then the function just returns the same object as is. More...

Protected Attributes
Constant Property	DEFAULT_RHO = 0.8

Constant Property	DEFAULT_P_CONST_FACT = 1.4

Protected Attributes inherited from matfaust::factparams::ParamsHierarchical
Constant Property	DEFAULT_IS_FACT_SIDE_LEFT = false

Protected Attributes inherited from matfaust::factparams::ParamsFact
Constant Property	DEFAULT_STEP_SIZE = 10

Constant Property	DEFAULT_VERBOSITY = false

Constant Property	DEFAULT_CONSTANT_STEP_SIZE = false

Constant Property	DEFAULT_INIT_LAMBDA = 1.0

Constant Property	DEFAULT_IS_UPDATE_WAY_R2L = false

Constant Property	DEFAULT_PACKING_RL = true

Constant Property	DEFAULT_FACTOR_FORMAT = 'dynamic'

Constant Property	DEFAULT_NO_NORMALIZATION = false

Constant Property	DEFAULT_NO_LAMBDA = false

Constant Property	DEFAULT_NORM2_MAX_ITER = 0

Constant Property	DEFAULT_NORM2_THRESHOLD = 0

Constant Property	IDX_FACTOR_FORMAT = 9

Constant Property	IDX_PACKING_RL = 10

Constant Property	IDX_NO_NORMALIZATION = 11

Constant Property	IDX_NO_LAMBDA = 12

Additional Inherited Members
Public Attributes inherited from matfaust::factparams::ParamsFact
Property	step_size

Property	constant_step_size

Property	factor_format

Property	packing_RL

Property	norm2_max_iter

Property	norm2_threshold

Property	use_MHTP

Property	no_normalization

Property	no_lambda

Detailed Description

The simplified parameterization class for factorizing a rectangular matrix with the hierarchical factorization algorithm.

Constructor & Destructor Documentation

◆ ParamsHierarchicalRectMat()

function matfaust::factparams::ParamsHierarchicalRectMat::ParamsHierarchicalRectMat	(	m	,
		n	,
		j	,
		k	,
		s	,
		varargin
	)

Constructor for the specialized parameterization used for example in the matfaust.demo.bsl (brain souce localization). For a better understanding you might refer to [1].

The figure below describes the sparsity of each factor of the Faust you'll obtain using pyfaust.fact.hierarchical with a ParamsHierarchicalRectMat instance.

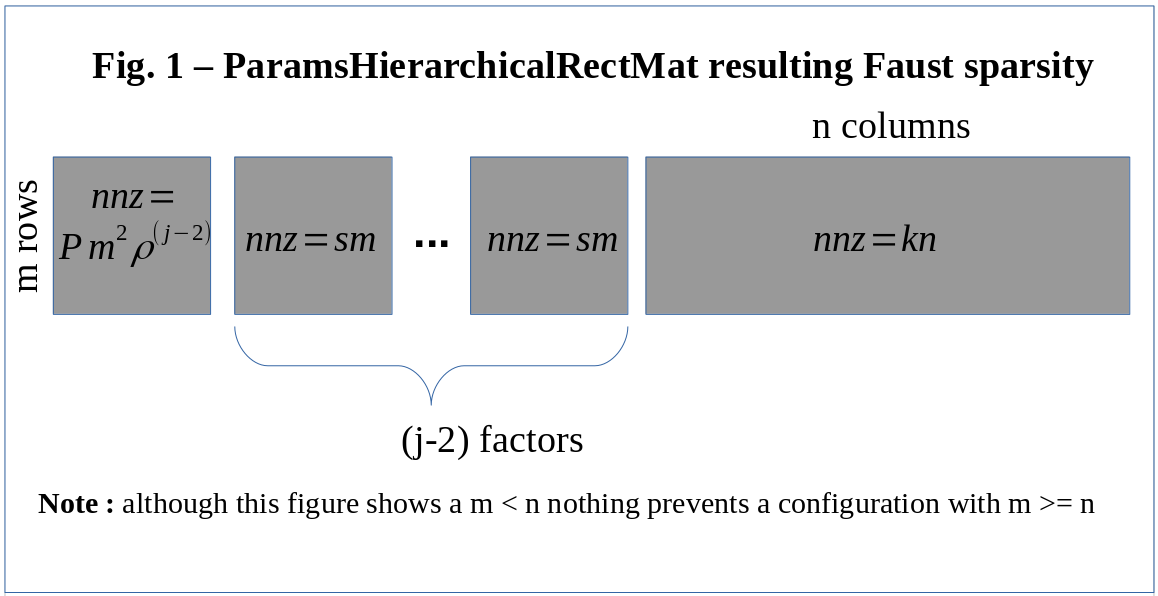
The resulting Faust.nnz_sum is: \( \lceil P m^2 \rho^{j-2} \rceil + (j-2) s m + k n \)

Parameters

m	the number of rows of the input matrix.
n	the number of columns of the input matrix.
j	the total number of factors.
k	the integer sparsity per column (SPCOL, matfaust.proj.spcol) applied to the rightmost factor (index j-1) of shape (m, n).
s	s*m is the integer sparsity targeted (SP, matfaust.proj.sp) for all the factors from the second (index 1) to index j-2. These factors are square of order n.
'rho',real	defines the integer sparsity (SP, matfaust.proj.sp) of the i-th residual (i=0:j-2): ceil(Pm^2rho^i).
'P',real	(default value is ParamsHierarchicalRectMat.DEFAULT_P_CONST_FACT) defines the integer sparsity of the i-th residual (i=0:j-2): ceil(Pm^2rho^i).

Example:

>> import matfaust.factparams.*
>> % set p1 with m, n, j, k parameters
>> p1 = ParamsHierarchicalRectMat(32, 128, 8, 4, 2);
>> % now with additional optional rho and P
>> p2 =  ParamsHierarchicalRectMat(32, 128, 8, 4, 2, 'rho', .7, 'P', 1.5);

[1] Le Magoarou L. and Gribonval R., "Flexible multi-layer sparse approximations of matrices and applications", Journal of Selected Topics in Signal Processing, 2016. [https://hal.archives-ouvertes.fr/hal-01167948v1]

Member Function Documentation

◆ createParams()

static function matfaust::factparams::ParamsHierarchicalRectMat::createParams	(	M	,
		p
	)

static

Static member function to create a ParamsHierarchicalRectMat instance by a simplified parameterization expression.

Parameters

p	a list of the form {'rectmat', j, k, s} or {'rectmat', j, k, s, 'rho', rho, 'P', P} to create a parameter instance with the parameters j, k, s and optionally rho and P (see the class constructor ParamsHierarchicalRectMat.ParamsHierarchicalRectMat for their definitions).

Example

>> import matfaust.factparams.ParamsHierarchicalRectMat
>> num_facts = 9;
>> k = 10;
>> s = 8;
>> p = ParamsHierarchicalRectMat.createParams(rand(256, 1024), {'rectmat', num_facts, k, s});
>> p2 = ParamsHierarchicalRectMat.createParams(rand(256, 1024), {'rectmat', num_facts, k, s, 'rho', 1.2, 'P', 2});

Member Data Documentation

◆ DEFAULT_P_CONST_FACT

Constant Property matfaust::factparams::ParamsHierarchicalRectMat::DEFAULT_P_CONST_FACT = 1.4

protected

◆ DEFAULT_RHO

Constant Property matfaust::factparams::ParamsHierarchicalRectMat::DEFAULT_RHO = 0.8

protected

The documentation for this class was generated from the following file:

ParamsHierarchicalRectMat.m

Public Member Functions

Static Public Member Functions

Protected Attributes

Additional Inherited Members